매력적인 Scala, 하지만 우리는 Go!
시간은 늘 그래왔듯이 잘 흘러간다. 객체지향적인 Go 프로그래밍이란? 글을 쓴지 거의 한달이 되었다. 아쉽게도 하루 일과에서 차지하는 비중이 낮아 배우는 속도는 더디다. 그럼에도 불구하고 조금씩 전진한 내용을 남겨본다. 최초에는 다른 이에게 공유할 수 있는 글을 쓰려고 노력했으나, 쓰다보니 배경지식이나 우리가 공유하는 맥락까지 설명하기는 어려워 힘을 좀 빼기로 했다. 친절한 전달보다는 기록에 더 의미를 둔 글임을 밝혀둔다.
우연히 만난 모범 답안
객체지향적인 Go 프로그래밍이란? 에 공유한 코드는 결과적으로는 모호한 코드였다. 그 의미는 아래와 같은 의문에 대한 답일 뿐이었다.
- Go는 클래스를 만들 수 없고, 상속이란 개념이 없는다. 그렇다면, 어떻게 다형성polymorphism을 실현할 수 있을까?
- 함수와 구조체(struct)만으로 조합 하다보면 적절한 조합단위가 필요할텐데?
- 함수형 언어나 Go와 같이 함수를 전면에 내세운 언어들을 다룰 때 유념할 설계 특성은 무엇인가?
- Java 경험 탓에 클래스 기반으로 사고하는 (나 같은) 사람에게
- 복잡한 업무를 객체 안에 켜켜이 내포시킨 경험이 없는 Go 개발자에게도
근데 얼마지나지 않아 우연한 계기로 Functional and Reactive Domain Modeling 이란 책이 눈에 띄었다. 사파리북에서 온라인으로 살만한 책인가 훑어 보는데 다음과 같은 예제가 등장했다.

출처: Functional and Reactive Domain Modeling
그리고, 해당 코드의 문제점이 제기된 후에 아래와 같은 개선 코드가 등장한다.

출처: Functional and Reactive Domain Modeling
나는 마치 학창시절 문제를 풀고 정답을 찾아볼 때와 같은 상황이 만들어진 느낌을 받았다. 막연한 희망사항을 Go 로 표현했던 경험이 문제를 푸는 과정이었다면, 우연히 찾은 책에서 살펴본 페이지는 그 대답같이 느껴졌다. 그래서, 책에서 찾은 정답을 요약하면 아래와 같다.
- 도메인 서비스[1] 단위로 함수를 묶고, 특정 객체의 상태값을 두지 않는 것이다. Scala[2]는 이를 지원하는 trait이라는 키워드가 있다.
- 다른 객체를 내포하는 형태인 Aggregate[3]가 필요한 상황이라면, 상태를 유지하지 않고 매번 새로 생성하도록 구현하라. 이는 일종의 ADT Algebraic Data Type 구현이다. (이건 뒤에 설명하겠다.)
책에 있는 간결한 도식을 공유한다.

출처: Functional and Reactive Domain Modeling
Abstract Data Type이 아니고 Algebraic Data Type?
거기까지 읽으니 알듯 모를듯한 힌트가 던져진 느낌을 받았다. 다만, ADT라는 말이 난제였다. 반나절인지 한나절인지를 Wikipedia 내용과 씨름을 했다.
In computer programming, especially functional programming and type theory, an algebraic data type is a kind of composite type, i.e., a type formed by combining other types. Two common classes of algebraic types are product types (i.e., tuples and records) and sum types, also called tagged or disjoint unions or variant types.
ADT 정의만 봐선 뭘 알기 힘들다. 체인처럼 다른 개념들, 이를 테면 Sum Type 이나 Product Type 등을 따라가며 학습해야 하는데 온통 수학이다! 이제와서 부족한 수학 바탕을 닦을 수는 없고, 내식대로 UML 클래스도를 그리면 대략 감을 잡으려고 시도했다.
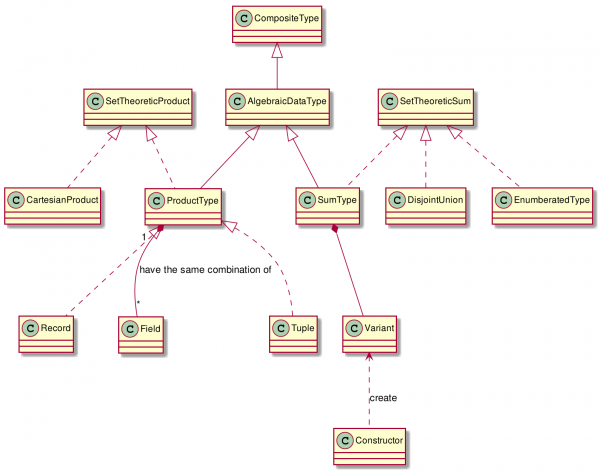
ADT 구성 도해
클래스도를 그리면 대강의 윤곽은 알 수 있다. 연관된 개념이 무엇이고, 대강의 관계를 한 눈에 볼 수 있다. 하지만, 부족한 해당 도메인에 대한 통찰이 구성도 그린다고 생기는건 아니다. 다행히 옆에 수학 기반이 탄탄한 임춘봉님이 있어서 머리속에 있는 내용을 나누었다. 그랬더니 ADT를 '합과 곱이네' 라고 단순하게 정의하셨다. 이 알쏭달쏭한 짧은 말이, 또 다시 나를 '왜 함수형 프로그래밍을 해야 하는가'하는 문제로 이끌었다.
함수형 프로그래밍이 필요한 경우
함수형으로 개발해본 일이 없다. 그저 Go를 쓰면서도 객체지향의 이점을 어떻게 살려낼까라는 질문에서 시작된 여행이다. 두번째 행선지가 도달한 곳은 놀랍게도 뜻밖에 발견한 책과 그 책이 소개한 수학개념들을 설명하는 위키피디아였는데, 이곳들을 여행하면서 퍼뜩 깨달은 바는 아래와 같다.
함수와 ADT는 한 쌍이다. 그리고, 입력이 같으면 늘 같은 결과값이 나와야 함수다.
편의상 필자가 과거에 올린 그림을 인용한다. 함수의 한 예이다. 빨간 색 선이 개발자가 작성하는 함수라면 파란색 점이 함수의 매개변수로 전달되는 인자이고, 연두색 점이 반환 값이다. ADT는 이러한 함수가 의미있게 쓰이기 위한 데이터 유형이며, 복합적인 값이기도 하다. 위 클래스도에서 CompositeType이라는 표현이 그것을 지칭하기도 하고, 포함 관계로 그려진 Field와 Variant가 달려 있음이 '복합적'이란 말의 복선이기도 하다.

출처: http://mcfunley.com/choose-boring-technology
다시 전진
여기까지 공부한 내용을 장재휴님과 나눴다. 그는 또 나를 통해 전달받은 자극을 이용해 Go로 자기 작품을 만들고 싶은 열망에 휩싸였다. 물론, 이해한 바를 얼마나 구현할 수 있을까 하는 긴장감도 느끼는 듯했다. 그 후 git 기반의 사내 리포지토리에 관련 코드와 이슈가 쌓이기 시작했다.
한편, 나는 책에서 보여준 코드 예제덕분에 Scala의 선명한 표현력에 매력을 느끼지 않을 수 없었다. 그렇지만, 우리는 지금 Go를 쓴다. 그래서, 우리 이야기는 계속된다. 그에 대한 이야기는 또 짬이 나면 쓰도록 하겠다.
주석
[1] 도메인은 설계/개발자가 관심을 두는 영역을 말하지만, 도메인 서비스는 Domain-Driven Design에서 포착한 일종의 패턴 이름이다. 핵심 특징은 (1) 클라이언트 프로그램을 위한 행위만 정의하며, (2) 상태를 내포하지 않는다는 점이다.
[2] 필자는 Scala를 모르는 상태로 책을 봤다. 당연히 이 글을 읽는데도 Scala를 알 필요는 없다.
[3] 역시 Domain-Driven Design에 등장하는 패턴인데, 엔티티 테이블과 연관관계를 갖는 테이블 묶음을 감싼encapsulation 객체라고 할 수 있다.